Category Archives: Uncategorized

Quantifying dispersion under varying instrument precision

Experimental errors are common at the moment of generating new data. Often this type of errors are simply due to the inability of the instrument to make precise measurements. In addition, different instruments can have different levels of precision, even-thought they are used to perform the same measurement. Take for example two balances and an object with a mass of 1kg. The first balance, when measuring this object different times might record values of 1.0083 and 1.0091, and the second balance might give values of 1.1074 and 0.9828. In this case the first balance has a higher precision as the difference between its measurements is smaller than the difference between the measurements of balance two.

In order to have some control over this error introduced by the level of precision of the different instruments, they are labelled with a measure of their precision $1/\sigma_i^2$ or equivalently with their dispersion $\sigma_i^2$ .

Let’s assume that the type of information these instruments record is of the form $X_i=C + \sigma_i Z$ , where $Z \sim N(0,1)$ is an error term, $X_i$ its the value recorded by instrument $i$ and where $C$ is the fixed true quantity of interest the instrument is trying to measure. But, what if $C$ is not a fixed quantity? or what if the underlying phenomenon that is being measured is also stochastic like the measurement $X_i$ . For example if we are measuring the weight of cattle at different times, or the length of a bacterial cell, or concentration of a given drug in an organism, in addition to the error that arises from the instruments; there is also some noise introduced by dynamical changes of the object that is being measured. In this scenario, the phenomenon of interest, can be given by a random variable $Y \sim N(\mu,S^2)$ . Therefore the instruments would record quantities of the form $X_i=Y + \sigma_i Z$ .

Under this case, estimating the value of $\mu$ , the expected state of the phenomenon of interest is not a big challenge. Assume that there are $x_1,x_2,...,x_n$ values observed from realisations of the variables $X_i \sim N(\mu, \sigma_i^2 + S^2)$ , which came from $n$ different instruments. Here $\sum x_i /n$ is still a good estimation of $\mu$ as $E(\sum X_i /n)=\mu$ . Now, a more challenging problem is to infer what is the underlying variability of the phenomenon of interest $Y$ . Under our previous setup, the problem is reduced to estimating $S^2$ as we are assuming $Y \sim N(\mu,S^2)$ and that the instruments record values of the from $X_i=Y + \sigma_i Z$ .

To estimate $S^2$ a standard maximum likelihood approach could be used, by considering the likelihood function:

$f(x_1,x_2,..,x_n)= \prod e^{-1/2 \times (x_i-\mu)^2 /(\sigma_i^2+S^2)} \times 1/\sqrt{2 \pi (\sigma_i^2+S^2) }$ ,

from which the maximum likelihood estimator of $S^2$ is given by the solution to

$\sum [(X_i- \mu)^2 - (\sigma_i^2 + S^2)] /(\sigma_i^2 + S^2)^2 = 0$ .

Another more naive approach could use the following result

$E[\sum (X_i-\sum X_i/n)^2] = (1-1/n) \sum \sigma_i^2 + (n-1) S^2$

from which $\hat{S^2}= (\sum (X_i-\sum X_i/n)^2 - ( (1-1/n ) \sum(\sigma_i^2) ) ) / (n-1)$ .

Here are three simulation scenarios where 200 $X_i$ values are taken from instruments of varying precision or variance $\sigma_i^2, i=1,2,...,200$ and where the variance of the phenomenon of interest $S^2=1500$ . In the first scenario $\sigma_i^2$ are drawn from $[10,1500^2]$ , in the second from $[10,1500^2 \times 3]$ and in the third from $[10,1500^2 \times 5]$ . In each scenario the value of $S_2$ is estimated 1000 times taking each time another 200 realisations of $X_i$ . The values estimated via the maximum likelihood approach are plotted in blue, and the values obtained by the alternative method are plotted in red. The true value of the $S^2$ is given by the red dashed line across all plots.

First simulation scenario where $\sigma_i^2, i=1,2,...,200$ in $[10,1500^2]$ . The values of $\sigma_i^2$ plotted in the histogram to the right. The 1000 estimations of $S$ are shown by the blue (maximum likelihood) and red (alternative) histograms.

First simulation scenario where $\sigma_i^2, i=1,2,...,200$ in $[10,1500^2 \times 3]$ . The values of $\sigma_i^2$ plotted in the histogram to the right. The 1000 estimations of $S$ are shown by the blue (maximum likelihood) and red (alternative) histograms.

First simulation scenario where $\sigma_i^2, i=1,2,...,200$ in $[10,1500^2 \times 5]$ . The values of $\sigma_i^2$ plotted in the histogram to the right. The 1000 estimations of $S$ are shown by the blue (maximum likelihood) and red (alternative) histograms.

For recent advances in methods that deal with this kind of problems, you can look at:

Delaigle, A. and Hall, P. (2016), Methodology for non-parametric deconvolution when the error distribution is unknown. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 78: 231–252. doi: 10.1111/rssb.12109

Conformational Variation of Protein Loops

Something many structural biologists (including us here in OPIG!) are guilty of is treating proteins as static, rigid structures. In reality, proteins are dynamic molecules, transitioning constantly from conformation to conformation. Proteins are therefore more accurately represented by an ensemble of structures instead of just one.

In my research, I focus on loop structures, the regions of a protein that connect elements of secondary structure (α-helices and β-sheets). There are many examples in the PDB of proteins with identical sequences, but whose loops have different structures. In many cases, a protein’s function depends on the ability of its loops to adopt different conformations. For example, triosephosphate isomerase, which is an important enzyme in the glycolysis pathway, changes conformation upon ligand binding, shielding the active site from solvent and stabilising the intermediate compound so that catalysis can occur efficiently. Conformational variability helps triosephosphate isomerase to be what is known as a ‘perfect enzyme’; catalysis is limited only by the diffusion rate of the substrate.

Structure of the triosephosphate isomerase enzyme. When the substrate binds, a loop changes from an ‘open’ conformation (pink, PDB entry 1TPD) to a ‘closed’ one (green, 1TRD), which prevents solvent access to the active site and stabilises the intermediate compound of the reaction.

An interesting example, especially for some of us here at OPIG, is the antibody SPE7. SPE7 is multispecific, meaning it is able to bind to multiple unrelated antigens. It achieves this through conformational diversity. Four binding site conformations have been found, two of which can be observed in its unbound state in equilibrium – one with a flat binding site, and another with a deep, narrow binding site [1].

An antibody that exists as two different structures in equilibrium - one with a shallow binding site (left, blue, PDB code 1OAQ) and one with a deep, narrow cleft (right, green, PDB 1OCW). Complementary determining regions are coloured in each case.

SPE7; an antibody that exists as two different structures in equilibrium – one with a shallow binding site (left, blue, PDB code 1OAQ) and one with a deep, narrow cleft (right, green, PDB 1OCW). Complementary determining regions are coloured in each case.

So when you’re dealing with crystal structures, beware! X-ray structures are averages – each atom position is an average of its position across all unit cells. In addition, thanks to factors such as crystal packing, the conformation that we see may not be representative of the protein in solution. The examples above demonstrate that the sequence/structure relationship is not as clear cut as we are often lead to believe. It is important to consider dynamics and conformational diversity, which may be required for protein function. Always bear in mind that the static appearance of an X-ray structure is not the reality!

[1] James, L C, Roversi, P and Tawfik, D S. Antibody Multispecificity Mediated by Conformational Diversity. Science (2003), 299, 1362-1367.

“Identifying Allosteric Hotspots with Dynamics”: Using molecular simulation to find critical sites for the functional motions in proteins

Allosteric (allo-(“other”) + steric (repulsion of atoms due to closeness or arrangement)) sites regulate protein function from a position other than the active site or binding site. Consider the latch on a pair of gardening scissors (Figure 1): depending on the position of the latch (allosteric site) the blades are prevented from cutting things at the other end (active site).

Figure 1 Allostery explained: A safety latch in gardening scissors.

Due to the non-trivial positions of allosteric sites in proteins their identification has been challenging. Selected well characterised systems such as GPCRs have known allosteric sites that are being used as targets in drug development. However, large scale identification of allosteric sites across the Protein Data Base (PDB) has not yet been feasible, partly because of the lack of tools.

To tackle this problem the Gerstein Lab developed a computational protocol based on various molecular simulations and network methods to find allosteric hotspots in proteins across the PDB. They introduce two different pipelines; one for identifying allosteric residues on the surface (surface-critical) and one for buried residues (interior-critical).

For the search of exterior-critical residues they us MC simulations to repeatedly probe the surface of the protein with short Monte Carlo (MC) with a short peptide. Based on hard spheres and simple energy calculations this method seems to be an efficient way of detecting possible binding pockets. Once the binding pockets have been found, the collective motions of the structure are simulated using an elastic mass-and-spring network (an anisotropic network model [ANM]). Binding pockets that undergo significant deformation during these simulations are considered to be surface-critical.

For interior-critical residues they start by weighting residue-residue contacts on the basis of collective movement. Communities within the weighted network are then identified and the residues with the highest betweenness interactions between communities are chosen as interior-critical residues. Thus, interior-critical residues have the highest information flow between two densely inter-connected groups of residues.

The protocol as been implemented in STRESS (STRucturally identified ESSential residues) and is freely available at stress.molmovdb.org.

Publication: http://www.ncbi.nlm.nih.gov/pubmed/27066750

Visualising Biological Data, Pt. 2

Here’s a little quick round-up of some of the tools/algorithms that I’ve seen in VIZBI, which I believe can be useful for many. For more details, I strongly advise you check out the posters page (vizbi.org/Posters/2016). There were a few that I would’ve liked to re-visit, but the webapps weren’t available (e.g. MeshCloud from the Human Genome Center, Tokyo), so maybe I’ll come back with a part 3. Here are my top five:

1. Autodesk’s Protein Viewer* (shout-outs to @_merrywang on Twitter)
As a structural bioinformatician, I’m going to be really biased here, and say that Autodesk’s Molecule viewer was the best tool that was showcased in the conference. It combines not only the capacity to visualise millions of molecules from the PDB (or your own PDB files), it also allows annotation and sharing, effectively, “snapshots” of your workspace for collaboration (see this if you want to know what I mean). AND it’s free! It’s not the fastest viewer on the planet, nor the easiest thing to use, but it is effective.

2. Vectorbase
Not related to protein structures, but a really interesting visualisation that shows information on, for example, insecticide resistance. With mosquitoes being such a huge part of today’s news, this kind of information is vital for fighting and understanding the distribution of insects across the globe.

3. Phandango
This is a genome browser which, from a one-man effort, could be a game-changer. The UI needs a little bit of work I think, but otherwise, a really valuable tool for crunching lots of genomic data in a quick fashion.

4. i-PV Circos
This is a neat circular browser that helps users view protein sequences in a circularised format. With this visualisation format becoming more popular as the days go by, I think this has the potential to be a leader in the field. At the moment the website’s a bit dark and not the most user-friendly, but some of the core functionality (e.g. highlighting residues and association of domains) is a real plus!

5. Storyline visualisation
Possibly my favourite/eye-opener tool from the entire conference. Storyline visualisation helps users understand how things progress in realtime — this has been used for movie plot data (e.g. Star Wars character and plot progression) but the general concept can be useful for biological phenomena – for example, how do cells in diseased states progress over time? How does it compare to healthy states? Can we also monitor protein dynamics using a similar concept? I think the fact that it gives a very intuitive, big-picture overview of the micro-scale dynamics was the reason why I’ve been incredibly interested in Kwan-Liu Ma’s work, and I recommend checking out his website/publications list to grab insight on improving data visualisation (in particular, network visualisation when you want to avoid hairballs!)

The list isn’t ranked in any way, and do check these out! There were other tools I would’ve really liked to review (e.g. Minardo, made by David Ma @frostickle on Twitter), but I suppose I can go on and on. At the end of the day, visualisation tools like these are meant to be quick, and help us to not only EXPLORE our data, but to EXPLAIN it too. I think we’re incredibly fortunate to have some amazing minds out there who are willing to not only create these tools, but also make them available for all.

Journal Club: “Discriminative Chemical Patterns: Automatic and Interactive Design”

For Journal Club this week I decided to discuss the following paper by M. Rarey et al., which describes a method of using SMARTS patterns to discriminate between two sets of molecules. Link to paper here.

Given two sets of molecules can one generate a pattern that discriminates between two sets? This relates to a key question in drug design: can we predict whether molecules bind or not given a set of binders and a set of non-binders. The method is of particular interest because it makes use of data available, unlike conventional methods. However, for this technique to work, the correct molecular classification is required to discriminate between the two sets of molecules.

Originally molecules were classified using physiochemical properties for example, molecular weight or log P. However these classifications are too general and do not encompass enough molecular detail for accurate discrimination. An alternative is to using topological fingerprints. These encode a set the presence of a set of topological features using a series of bits. One of the limitations with this classification is that it is restricted by the predefined set of structures and features. This method makes use of chemical patterns which advantageously can can classify a chemical feature that cannot be sufficiently described by molecular substructure.

SMARTS (a molecular description language based on SMILES) allow description of structures with varying levels of specificity. For example one can specify atomic element, whether the atom is a subset of elements, whether it is aliphatic or aromatic, or whether it is in a ring. The method makes use of this description of molecules as the group have already developed some software to visualise SMARTS strings and modify them: the SMARTSeditor.

The method involves combining automatic pattern generation and visualisation to form SMARTSminer. Given two distinct molecule sets, the algorithm derives connected chemical patterns to differentiate both sets by using a sub-graph mining technique: solutions are extended by single elements iteratively.

The SMARTSminer was then used to test a series of test cases using the DUD (Database of Useful Decoys) data set. This seems strange when the data set has been shown to be inaccurate and perhaps there are more accurate test sets available, such as DUDe (Database of Useful Decoys enchanced). Let us look a couple of these case sets in more detail.

Discrimination between Active Molecules on Similar Targets

The first case set looks at discriminating between molecules that are active for COX-1 and COX-2. COX proteins are cyclooxygenase that are involved in inflammatory reaction. These proteins are targeted by inhibitors such as aspirin and ibuprofen for the relief of inflammatin and pain. Both COX-1 and COX-2 are similar targets with similar molecular weight and 65% sequence identity. Selective inhibition is only due to a difference in residue at position 523.

Separation of the sets of molecules was possible with a pattern identified that hit 21/25 of the molecules active for COX-1 and 15/348 of molecules of molecules active for COX-2. When the positive and negative set are reversed a pattern is identified that matched 313/348 of COX-2 actives but only 1 of the COX-1 ligands. The group state that perfect separation is not possible as there is an overlap of 2 molecules.

It is interesting that patterns were identified that could discriminate between the two sets. However, there is no discussion of how to use this information. Additionally the pattern determined has not been tested on any molecules outside of the training set – there are no blind tests. This seems strange as a blind test could emphasise the usefulness of this method if it was successful.

2. Discrimination between Active and Inactive Molecules

The second case investigates determining whether a pattern can be generated that discriminates between active and inactive targets. The test case used target SAHH (S-adenosyl-homocysteine hydrolase). A pattern was generated that matched all active molecules and only 1% of inactives. What is particularly exciting is that the pattern found contains part of the interaction network hydrogen bonding partners of the ligand, as shown in the figure below (the pattern identified is highlighted in green).

I find it very surprising that the group did not follow up with blind tests of molecules not used in the training set – especially as the pattern identified a key part of the binding mechanism.

To summarise a new method, SMARTSminer, calculates discriminative patterns between two sets of molecules using the SMARTS language. The authors state that the method has shown applicability in several use cases covering the application of actives vs decoys, kinase classifications, analysis of data sets and characterisation of reaction centers. However, I’m not sure I can agree with that statement. I believe further blind tests would be required to prove the applicability of the method once the pattern has been found. I also believe that an analysis of whether the pattern is over fitted to the training data is also required.

Visualising Biological Data, Pt. 1

Hey Blopig Readers,

I had the privilege to go down to Heidelberg last week to go and see some stunning posters and artwork. I really recommend that you check some of the posters out. In particular, the “Green Fluorescent Protein” poster stuck out as my favourite. Also, if you’re a real Twitter geek, check out #Vizbi for some more tweets throughout the week.

So what did the conference entail? As a very blunt summary, it was really an eclectic collection of researchers around the globe who showcased their research with very neat visual media. While I was hoping for a conference that gave an overview of some of the principles that dictate how to visualise proteins, genes, etc., it wasn’t like that at all! Although I was initially a bit disappointed, it turned out to be better – one of the key themes that were re-iterated throughout the conference is that visualisations are dependent on the application!

From the week, these are the top 5 lessons I walked away with, and I hope you can integrate this into your own visualisation:

There is no pre-defined, accepted way of visualising data. Basically, every visualisation is tailored, has a specific purpose, so don’t try to fit your graph into something pretty that you’ve seen in another paper. We’re encouraged to get insight from others, but not necessarily replicate a graph.
KISS (Keep it simple, stupid!) Occam’s razor, KISS, whatever you want to call it – keep things simple. Making an overly complicated visualisation may backfire.
Remember your colours. Colour is probably one of the most powerful tools in our arsenal for making the most of a visualisation. Don’t ignore them, and make sure that they’re clean, separate, and interpretable — even to those who are colour-blind!
Visualisation is a means of exploration and explanation. Make lots, and lots of prototypes of data visuals. It will not only help you explore the underlying patterns in your data, but help you to develop the skills in explaining your data.
Don’t forget the people. Basically, a visualisation is really for a specific target audience, not for a machine. What you’re doing is to encourage connections, share knowledge, and create an experience so that people can learn your data.

I’ll come back in a few weeks’ time after reviewing some tools, stay tuned!

Network Comparison

Why network comparison?

Many complex systems can be represented as networks, including friendships (e.g. Facebook), the World Wide Web trade relations and biological interactions. For a friendship network, for example, individuals are represented as nodes and an edge between two nodes represents a friendship. The study of networks has thus been a very active area of research in recent years, and, in particular, network comparison has become increasingly relevant. Network comparison, itself, has many wide-ranging applications, for example, comparing protein-protein interaction networks could lead to increased understanding of underlying biological processes. Network comparison can also be used to study the evolution of networks over time and for identifying sudden changes and shocks.

An example of a network.

How do we compare networks?

There are numerous methods that can be used to compare networks, including alignment methods, fitting existing models,
global properties such as density of the network, and comparisons based on local structure. As a very simple example, one could base comparisons on a single summary statistic such as the number of triangles in each network. If there was a significant difference between these counts (relative to the number of nodes in each network) then we would conclude that the networks are different; for example, one may be a social network in which triangles are common – “friends of friends are friends”. However, this a very crude approach and is often not helpful to the problem of determining whether the two networks are similar. Real-world networks can be very large, are often deeply inhomogeneous and have multitude of properties, which makes the problem of network comparison very challenging.

A network comparison methodology: Netdis

Here, we describe a recently introduced network comparison methodology. At the heart of this methodology is a topology-based similarity measure between networks, Netdis [1]. The Netdis statistic assigns a value between 0 and 1 (close to 1 for very good matches between networks and close to 0 for similar networks) and, consequently, allows many networks to be compared simultaneously via their Netdis values.

The method

Let us now describe how the Netdis statistic is obtained and used for comparison of the networks G and H with n and m nodes respectively.

For a network G, pick a node i and obtain its two-step ego-network. That is, the network induced by collection of all nodes in G that are connected to i via a path containing at most two edges. By induced we mean that a edge is present in the two-step ego-network of i if and only if it is also present in the original network G. We then count the number of times that various subgraphs occur in the ego-network, which we denote by $N_{w,i}(G)$ for subgraph w. For computational reasons, this is typically restricted to subgraphs on 5 or fewer nodes. This processes is repeated for all nodes in G, for fixed k=3,4,5.

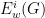Under an appropriately chosen null model, an expected value for the quantities $N_{w,i}(G)$ is given, denoted by $E_w^i(G)$ . We omit some of these details here, but the idea is to centre the quantities $N_{w,i}(G)$ to remove background noise from an individual networks.
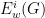Under an appropriately chosen null model, an expected value for the quantities $N_{w,i}(G)$ is given, denoted by $E_w^i(G)$ . We omit some of these details here, but the idea is to centre the quantities $N_{w,i}(G)$ to remove background noise from an individual networks.
Calculate:
To compare networks G and H, define:where A(k) is the set of all subgraphs on k nodes andis a normalising constant that ensures that the statistic $netD_2^S(k)$ takes values between -1 and 1. The corresponding Netdis statistic is: which now takes values in the interval between 0 and 1.
The pairwise Netdis values from the equation above are then used to build a similarity matrix for all query networks. This can be done for any 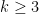$k \geq3$ , but for computational reasons, this typically needs to be limited to 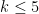$k\leq5$ . Note that for k=3,4,5 we obtain three different distance matrices.
The performance of Netdis can be assessed by comparing the nearest neighbour assignments of networks according to Netdis with a ‘ground truth’ or ‘reference’ clustering. A network is said to have a correct nearest neighbour whenever its nearest neighbour according to Netdis is in the same cluster as the network itself. The overall performance of Netdis on a given data set can then be quantified using the nearest neighbour score (NN), which for a given set of networks is defined to be the fraction of networks that are assigned correct nearest neighbours by Netdis.

The phylogenetic tree obtained by Netdis for protein interaction networks. The tree agrees with the currently accepted phylogeny between these species.

Why Netdis?

The Netdis methodology has been shown to be effective at correctly clustering networks from a variety of data sets, including both model networks and real world networks, such Facebook. In particular, the methodology allowed for the correct phylogenetic tree for five species (human, yeast, fly, hpylori and ecoli) to be obtained from a Netdis comparison of their protein-protein interaction networks. Desirable properties of the Netdis methodology are the following:

\item The statistic is based on counts of small subgraphs (for example triangles) in local neighbourhoods of nodes. By taking into account a variety of subgraphs, we capture the topology more effectively than by just considering a single summary statistic (such as number of triangles). Also, by considering local neighbourhoods, rather than global summaries, we can often deal more effectively with inhomogeneous graphs.

The Netdis statistic contains a centring by subtracting background expectations from a null model. This ensures that the statistic is not dominating by noise from individual networks.
The statistic also contains a rescaling to ensure that counts of certain commonly represented subgraphs do not dominate the statistic. This also allows for effective comparison even when the networks we are comparing have a different number of nodes.
The statistic is normalised to take values between 0 and 1 (close to 1 for very good matches between networks and close to 0 for similar networks). The statistic gives values between 0 and 1 and based on this number, we can simultaneously compare many networks; networks with Netdis value close to one can be clustered together. This offers the possibility of network phylogeny reconstruction.

A new variant of Netdis: subsampling

The performance of Netdis under subsampling for a data set consisting of protein interaction networks. The performance of Netdis starts to deteriorate significantly only after less than 10% of ego networks are sampled.

Despite the power of Netdis as an effective network comparison method, like many other network comparison methods, it can become computationally expensive for large networks. In such situations the following variant of Netdis may be preferable (see [2]). This variant works by only querying a small subsample of the nodes in each network. An analogous Netdis statistic is then computed based on subgraph counts in the two-step ego networks of the sampled nodes. From numerous simulation studies and experimentations, it has been shown that this statistic based on subsampling is almost as effective as Netdis provided that at least 5 percent of the nodes in each network are sampled, with the new statistic only really dropping off significantly when fewer than 1 percent of nodes are sampled. Remarkably, this procedure works well for inhomogeneous real-world networks, and not just for networks realised from classical homogeneous random graphs, in which case one would not be surprised that the procedure works.

Other network comparison methods

Finally, we note that Netdis is one of many network comparison methodologies present in the literature Other popular network comparison methodologies include GCD [3], GDDA [4], GHOST [5], MI-Graal [6] and NETAL [7].

[1] Ali W., Rito, T., Reinert, G., Sun, F. and Deane, C. M. Alignment-free protein
interaction network comparison. Bioinformatics 30 (2014), pp. i430–i437.

[2] Ali, W., Wegner, A. E., Gaunt, R. E., Deane, C. M. and Reinert, G. Comparison of
large networks with sub-sampling strategies. Submitted, 2015.

[3] Yaveroglu, O. N., Malod-Dognin, N., Davis, D., Levnajic, Z., Janjic, V., Karapandza,
R., Stojmirovic, A. and Prˇzulj, N. Revealing the hidden language of complex networks. Scientific Reports 4 Article number: 4547, (2014)

[4] Przulj, N. Biological network comparison using graphlet degree distribution. Bioinformatics 23 (2007), pp. e177–e183.

[5] Patro, R. and Kingsford, C. Global network alignment using multiscale spectral
signatures. Bioinformatics 28 (2012), pp. 3105–3114.

[6] Kuchaiev, O. and Przulj, N. Integrative network alignment reveals large regions of
global network similarity in yeast and human. Bioinformatics 27 (2011), pp. 1390–
1396.

[7] Neyshabur, B., Khadem, A., Hashemifar, S. and Arab, S. S. NETAL: a new graph-
based method for global alignment of protein–protein interaction networks. Bioinformatics 27 (2013), pp. 1654–1662.

Community structure in multilayer networks

Multilayer networks are a generalisation of network that may incorporate different types of interactions [1]. This could be different time points in temporal data, measurements in different individuals or under different experimental conditions. Currently many measures and methods from monolayer networks are extended to be applicabile to multilayer networks. Those include measures of centrality [2], or methods that enable to find mesoscale structure in networks [3,4].

Examples of such mesoscale structure detection methods are stochastic block models and community detection. Both try to find groups of nodes that behave structurally similar in a network. In its most simplistic way you might think of two groups that are densely connected internally but only sparsely between the groups. For example two classes in a high school, there are many friendships in each class but only a small number between the classes. Often we are interested in how such patterns evolve with time. Here, the usage of multilayer community detection methods is fruitful.

From [4]: Multislice community detection of U.S. Senate roll call vote similarities across time. Colors indicate assignments to nine communities of the 1884 unique senators (sorted vertically and connected across Congresses by dashed lines) in each Congress in which they appear. The dark blue and red communities correspond closely to the modern Democratic and Republican parties, respectively. Horizontal bars indicate the historical period of each community, with accompanying text enumerating nominal party affiliations of the single-slice nodes (each representing a senator in a Congress): PA, pro-administration; AA, anti-administration; F, Federalist; DR, Democratic-Republican; W, Whig; AJ, anti-Jackson; A, Adams; J, Jackson; D, Democratic; R, Republican. Vertical gray bars indicate Congresses in which three communities appeared simultaneously.

Mucha et al. analysed the voting pattern in the U.S. Senate [4]. They find that the communities are oriented as the political party organisation. However, the restructuring of the political landscape over time is observable in the multilayered community structure. For example, the 37th Congress during the beginning of the American Civil War brought a major change in the voting patterns. Modern politics is dominated by a strong partition into Democrats and Republicans with third minor group that can be identified as the ‘Southern Democrats’ that had distinguishable voting patterns during the 1960.

Such multilayer community detection methods can be insightful for networks from other disciplines. For example they have been adopted to describe the reconfiguration in the human brain during learning [5]. Hopefully they will be able to give us insight in the structure and function of protein interaction.

[1] De Domenico, Manlio; Solé-Ribalta, Albert; Cozzo, Emanuele; Kivelä, Mikko; Moreno, Yamir; Porter, Mason A.; Gómez, Sergio; and Arenas, Alex [2013]. Mathematical Formulation of Multilayer Networks, Physical Review X, Vol. 3, No. 4: 041022.

[2] Taylor, Dane; Myers, Sean A.; Clauset, Aaron; Porter, Mason A.; and Mucha, Peter J. [2016]. Eigenvector-based Centrality Measures for Temporal Networks

[3] Tiago P. Peixoto; Inferring the mesoscale structure of layered, edge-valued, and time-varying networks. Phys. Rev. E 92, 042807

[4] Mucha, Peter J.; Richardson, Thomas; Macon, Kevin; Porter, Mason A.; and Onnela, Jukka-Pekka [2010]. Community Structure in Time-Dependent, Multiscale, and Multiplex Networks, Science, Vol. 328, No. 5980: 876-878.

[5] Bassett, Danielle S.; Wymbs, Nicholas F.; Porter, Mason A.; Mucha, Peter J.; Carlson, Jean M.; and Grafton, Scott T. [2011]. Dynamic Reconfiguration of Human Brain Networks During Learning, Proceedings of the National Academy of Sciences of the United States of America, Vol. 118, No. 18: 7641-7646.

Inserting functional proteins in an antibody

At the group meeting on the 3rd of February I presented the results of the paper “A General Method for Insertion of Functional Proteins within Proteins via Combinatorial Selection of Permissive Junctions” by Peng et. al. This is interesting to our group, and especially to me, because this is a novel way of designing an antibody, although I suspect that the scope of their research is much more general, their use of antibodies being a proof of concept.

Their premise is that the structure of a protein is essentially secondary structures and tertiary structure interconnected through junctions. As such it should be possible to interconnect regions from different proteins through junctions, and these regions should take up their native secondary and tertiary structures, thus preserving their functionality. The question is what is a suitable junction? This is important because these junctions should be flexible enough to allow the proper folding of the different regions, but also not too flexible as to have a negative impact on stability. There has been previous work done on trying to design suitable junctions, however the workflow presented in this paper is based on trying a vast number of junctions and then identifying which of them work.

As I said above their proof concept is antibodies. They used an antibody scaffold (the host), out of which they removed the H3 loop and then fused to it, using junctions, two different proteins: Leptin and FSH (the guests). To identify the correct junctions they generated a library of antibodies with random three residues sequences on either side of the inserted protein plus a generic linker (GGGGS) that can be repeated up to three times.

They say that the theoretical size of the library is 10^9 (however I would say it is 9*20^6), and the actually achieved diversity of their library was of size 2.88*10^7 for Leptin and 1.09*10^7. Next step is to identify which junctions have allowed the guest protein to fold properly. For this they devised an autocrine-based selection method using engineered cells that have beta lactamase receptors which have either Leptin or FSH as agonists. A fluoroprobe in the cell responds to the presence of beta lactamase producing a blue color, instead of green and therefore this allows the cells with the active antibody-guest designed protein (clone) to be identified using FRET-based fluorescence-activated cell sorting.

They managed to identify 6 clones that worked for Leptin and 3 that worked for FSH with the linkers being listed in the below table:

There does not seem to be a pattern emerging from those linker sequences, although one of them repeats itself. For my research it would have been interesting if a pattern did emerge, and then that could be used as a generic linker for future designers. However, this is still another prime example of how well an antibody scaffold can be used a starting point for protein engineering.

As a bonus they also tested in vivo how their designs work and they discovered that the antibody-leptin design (IgG-Leptin) has a longer lifetime. This is probably due to the fact that being a larger protein this is not filtered out by the kidneys.

Designing antibodies targeting disordered epitopes

At the meeting on February 10 I covered the article by Sormanni et al. describing a methodology for computationally designing antibodies against intrinsically disordered regions of proteins.

Antibodies are proteins that are a natural part of our immune system. For over 50 years lab-made antibodies have been used in a wide variety of therapeutic and diagnostic applications. Nowadays, we can design antibodies with high specificity and affinity for almost any target. Nevertheless, engineering antibodies against intrinsically disordered proteins remains costly and unreliable. Since as many as about 33.0% of all eukaryotic proteins could be intrinsically disordered, and the disordered proteins are often implicated in various ailments and diseases such methodology could prove invaluable.

Cascade design

The initial step in the protocol involves searching the PDB for protein sequences that interact in a beta strand with segments of the target sequence. Next, such peptides are joined together using a so-called “cascade method”. The cascade method starts with the longest found peptide and grows it to the length of the target sequence by joining it with other, partially overlapping peptides coming from beta strands of the same type (parallel, antiparallel). In the cascade method, all fragments used must form the same hydrogen bond pattern. The resulting complementary peptide is expected to “freeze” part of the discorded protein by forcing it to locally form a beta sheet. After the complementary peptide is designed, it is grafted on a single-domain antibody scaffold. This decision has been made as antibodies have a longer half-life and lower immunogenicity.

To test their method the authors initially assessed the robustness of their design protocol. First, they run the cascade method on three targets – a-synuclein, Aβ42 and IAPP. They found that more than 95% of the residue position in the three proteins could be targeted by their method. In addition, the mean number of available fragments per position was 570. They also estimated their coverage on a larger scale, using 1690 disordered protein sequences obtained from DisProt database and from measured NMR chemical shifts. About 90% of residue positions from DisProt and 85% positions from the chemical shift could be covered by at least one designed peptide. The positions that were hard to target usually contained Proline, in agreement with the known result that Prolines tend to disrupt secondary structure formation.

To test the quality of their designs the authors created complementary peptides for a-synuclein, Aβ42 and IAPP and grafted them on the CDR3 region of a human single domain antibody scaffold. All designs were highly stable and bound their targets with high specificity. Following the encouraging result the authors measured the affinity of one of their designs (one of the anti-a-synuclein antibodies). The K_d was found to lie in the range 11-27 μM. Such affinity is too low for pharmaceutical purposes, but it is enough to prevent aggregation of the target protein.

As the last step in the project the authors attempted a two-peptide design, where a second peptide was grafted in the CDR2 region of the single-domain scaffold. Both peptides were designed to bind the same epitope. The two peptide design managed to reach the affinity required for pharmaceutical viability (affinity smaller than 185 nM with 95% confidence). Nevertheless, the two loop design became very unstable rendering it not viable for pharmaceutical purposes.

Overall, this study presents a very exciting step towards computationally designed antibodies targeting disordered epitopes and deepens out understanding of antibody functionality.

Oxford Protein Informatics Group

or "OPIG" to friends