Author Archives: Lyuba

Consistent plotting with ggplot

Unlike other OPIGlets (looking at you, Claire), I have neither the skill nor the patience to make good figures from scratch. And making good figures — as well as remaking, rescaling and adapting them — is incredibly important, because they play a huge role in the way we communicate our research. So how does an aesthetically impaired DPhil student do her plotting?

Continue reading →

Oxford Maths Festival ‘19

The Oxford Maths Festival returned this year and it was tons of fun, at least for this volunteer! I failed to take pictures, but a few opiglets were involved: Flo and company took their VR work for the Ashmolean Dimensions exhibit and demonstrated it at Templars Square, and Conor did a spectacular job pretending to be a police constable for the maths escape room.

Last year Mark blogged about how we demonstrated the German Tank Problem at the festival. I thought this time round I’d share another of the Mathematical Mayhem activities: a game illustrating biased sampling.

Continue reading →

Preparing a five minute conference talk: an honest account

On 26 September I had the opportunity to give a short talk at the COSTNET18 conference in Warsaw. I’d never done anything like it before, which made it both exciting and a tiny bit terrifying. I thought I’d share how I prepared for it, in the hope that other conference newbies might find some of it useful, or at least funny.

20 July

I register for the conference, and apply to give a talk. I use a version of my paper draft abstract, to which I add a couple of introductory sentences. I submit successfully, but at the end of the day accidentally delete this version of the abstract from my computer. I guess if I need it, I just need to wait until the conference programme becomes available. #fail Continue reading →

A short intro to machine precision and how to beat it

Most people who’ve ever sat through a Rounding Error is Bad lecture will be familiar with the following example:

> (0.1+0.1+0.1) == 0.3
FALSE

The reason this is so unsettling is because most of the time we think about numbers in base-10. This means we use ten digits $\{0, 1, \dots, 9\}$ , and we perform arithmetic based on this ten digit notation. This doesn’t always matter much for pen and paper maths but it’s an integral part of how we think about more complex operations and in particular how we think about accuracy. We see $0.1$ as a finite decimal fraction, and so it’s only natural that we should be able to do accurate sums with it. And if we can do simple arithmetic, then surely computers can too? In this blog post I’m going to try and briefly explain what causes rounding errors such as the one above, and how we might get away with going beyond machine precision.

Take a number $x \in [0; 1)$ , say $x=1/3$ . The decimal representation of $x$ is of the form $x=\sum_{i=1}^{\infty} a_i \times 10^{-i}$ . The $a_i \in \{0, 1, \dots, 9\}$ here are the digits that go after the radix point. In the case of $x=1/3$ these are all equal $a_i=3$ , or $x=0.333\dots _{10}$ . Some numbers, such as our favourite $x$ , don’t have a finite decimal expansion. Others, such as $0.3$ , do, meaning that after some $i \in \mathbb{N}$ , all $a_{i+j}=0$ . When we talk about rounding errors and accuracy, what we actually mean is that we only care about the first few digits, say $i\leq 5$ , and we’re happy to approximate to $x\approx \sum_{i=1}^{5} a_i \times 10^{-i}=0.33333$ , potentially rounding up at the last digit.

Computers, on the other hand, store numbers in base-2 rather than base-10, which means that they use a different series expansion $x=\sum_{i=1}^{\infty} b_i \times 2^{-i}$ , $b_i \in \{0, 1\}$ to represent the same number. Our favourite number $x$ is actually stored as $0.1010101\dots _{2}$ rather than $0.3333333\dots _{10}$ , despite the fact it appears as the latter on a computer screen. Crucially, arithmetic is done in base-2 and, since only a finite number of binary digits are stored ( $i\leq 52$ for most purposes these days), rounding errors also occur in base-2.

All numbers with a finite binary expansion, such as $0.25_{10}=0\times 1/2+1\times 1/4=0.01_{2}$ also have a finite decimal expansion, meaning we can do accurate arithmetic with them in both systems. However, the reverse isn’t true, which is what causes the issue with $0.1+0.1+0.1\neq 0.3$ . In binary, the nice and tidy $0.1_{10} = 0.00011001100\dots _{2}$ . We observe the rounding error because unlike us, the computer is trying to sum over infinite series.

While it’s not possible to do infinite sums with finite resources, there is a way to go beyond machine precision if you wanted to, at least for rational $x=p/q$ , where $p, q \in \mathbb{N}$ . In the example above, the issue comes from dividing by 10 on each side of the (in)equality. Luckily for us, we can avoid doing so. Integer arithmetic is easy in any base, and so

> (1+1+1) == 3 
TRUE

Shocking, I know. On a more serious note, it is possible to write an algorithm which calculates the binary expansion of $x=p/q$ using only integer arithmetic. Usually binary expansion happens in this way:

set x, maxIter
initialise b, i=1
while x>0 AND i<=maxIter {
 if 2*x>=1
    b[i]=1
 else
    b[i]=0
 x = 2*x-b[i]
 i = i+1 
}
return b

Problems arise whenever we try to compute something non-integer (the highlighted lines 3, 4, and 8). However, we can rewrite these using $x = p/q$ and shifting the division by $q$ to the right-hand side of each inequality / assignment operator:

set p, q, maxIter
initialise b, i=1 
while p>0 AND i<=maxIter { 
 if 2*p>=q 
    b[i]=1 
 else 
    b[i]=0 
 p = 2*p-b[i]*q 
 i = i+1 
} 
return b

Provided we’re not dealing with monstrously large integers (i.e. as long as we can safely double $p$ ), implementing the above lets us compute $p/q$ with arbitrary precision given by maxIter. So we can beat machine precision for rationals! And the combination of arbitrarily accurate rationals and arbitrarily accurate series approximations (think Riemann zeta function, for example) means we can also get the occasional arbitrarily accurate irrational.

To sum up, rounding errors are annoying, partly because it’s not always intuitive when and how they happen. As a general rule the best way to avoid them is to make your computer do as little work as possible, and to avoid non-integer calculations whenever you can. But you already knew that, didn’t you?

This post was partially inspired by the undergraduate course on Simulation and Statistical Programming lectured by Prof Julien Berestycki and Prof Robin Evans. It was also inspired by my former maths teacher who used to mark us down for doing more work than necessary even when our solutions were correct. He had a point.

Journal club: Human enterovirus 71 protein interaction network prompts antiviral drug repositioning

Viruses are small infectious agents, which possess genetic code but have no independent metabolism. They propagate by infecting host cells and hijacking their machinery, often killing the cells in the process. One of the key challenges in developing effective antiviral therapies is the high mutation rate observed in viral genomes. A way to circumvent this issue is to target host proteins involved in virion assembly (also known as essential host factors, or EHFs), rather than the virion itself.

In their recent paper, Lu Han et al. [1] consider human virus protein-protein interactions in order to explore possible host drug targets, as well as drugs which could potentially be re-purposed as antivirals. Their study focuses on enterovirus 71 (EV71), one of the leading causes of hand, foot, and mouth disease.

Human virus protein-protein interactions and target identification

EHFs are typically detected by knocking out genes in the host organism and determining which of the knockouts result in virus control. Low repeat rates and high costs make this technique unsuitable for large scale studies. Instead, the authors use an extensive yeast two-hybrid screen to identify 37 unique protein-protein interactions between 7 of the 11 virus proteins and 29 human proteins. Pathway enrichment suggests that the human proteins interacting with EV71 are involved in a wide range of functions in the cell. Despite this range in functionality, as many as 17 are also associated with other viruses, either through known physical interactions, or as EHFs (Fig 1).

Fig. 1. Interactions between viral and human proteins (denoted as EIPs), and their connection to different viruses.

One of these is ATP6V0C, a subunit of vacuole ATP-ase. It interacts with the EV71 3A protein, and is a known essential host factor for five other viruses. The authors analyse the interaction further, and show that downregulating ATP6V0C gene expression inhibits EV71 propagation, while overexpressing it enhances virus propagation. Moreover, treating cells with bafilomycin A1, a selective inhibitor for vacuole ATP-ase, inhibits EV71 infection in a dose-dependent manner. The paper suggests that therefore ATP6V0C may be a suitable drug target, not only against EV71, but also perhaps even for a broad-spectrum antiviral. While this is encouraging, bafilomycin A1 is a toxic antibiotic used in research, but not suitable for human or drug use. Rather than exploring other compounds targeting ATP6V0C, the paper shifts focus to re-purposing known drugs as antivirals.

Drug prediction using CMap

A potential antiviral will ideally disturb most or all interactions between host cell and virion. One way to do this would be to inhibit the proteins known to interact with EV71. In order to check whether any known compounds already do so, the authors apply gene set enrichment analysis (GSEA) to data from the connectivity map (CMap). CMap is a database of gene expression profiles representing cellular response to a set of 1309 different compounds. Enrichment analysis of the database reveals 27 potential EV71 drugs, of which the authors focus on the top ranking result, tanespimycin.

Tanespimycin is an orphan cancer drug, originally designed to target tumor cells by inhibiting HSP90. Its complex effects on the cell, however, may make it an effective antiviral. Following their CMap analysis, the authors show that tanespimycin reduces viral count and virus-induced cytopathic effects in a dose-dependent manner, without evidence of cytotoxicity.

Overall, the paper presents two different ways to think about target investigation and drug choice in antiviral therapeutics — by integrating different types of known host virus protein-protein interactions, and by analysing cell response to known compounds. While extensive further study is needed to determine whether the results are directly clinically relevant to the treatment of EV71, the paper shows how interaction data analysis can be employed in drug discovery.

References:

[1] Han, Lu, et al. “Human enterovirus 71 protein interaction network prompts antiviral drug repositioning.” Scientific Reports 7 (2017).

Confidence (scores) in STRING

There are many techniques for inferring protein interactions (be it physical binding or functional associations), and each one has its own quirks: applicability, biases, false positives, false negatives, etc. This means that the protein interaction networks we work with don’t map perfectly to the biological processes they attempt to capture, but are instead noisy observations.

The STRING database tries to quantify this uncertainty by assigning scores to proposed protein interactions based on the nature and quality of the supporting evidence. STRING contains functional protein associations derived from in-house predictions and homology transfers, as well as taken from a number of externally maintained databases. Each of these interactions is assigned a score between zero and one, which is (meant to be) the probability that the interaction really exists given the available evidence.

Throughout my short research project with OPIG last year I worked with STRING data for Borrelia Hermsii, a relatively small network of scored interactions across 815 proteins. I was working with v.10.0., the latest available database release, but also had the chance to compare this to v.9.1 data. I expected that with data from new experiments and improved scoring methodologies available, the more recent network would be more or less a re-scored superset of the older. Even if some low-scored interactions weren’t carried across the update, I didn’t expect these to be any significant proportion of the data. Interestingly enough, this was not the case.

Out of 31 264 scored protein-protein interactions in v.9.1. there were 10 478, i.e. almost exactly a third of the whole dataset, which didn’t make it across the update to v.10.0. The lost interactions don’t seem to have very much in common either — they come from a range of data sources and don’t appear to be located within the same region of the network. The update also includes 21 192 previously unrecorded interactions.

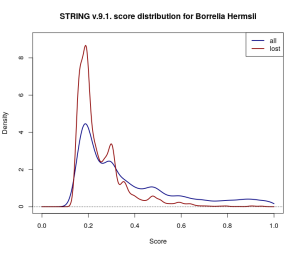
Gaussian kernel density estimates for the score distribution of interactions across the entire 9.1. Borrelia Hermsii dataset (navy) and across the discarded proportion of the dataset (dark red). Proportionally more low-scored interactions have been discarded.

Repeating the comparison with baker’s yeast (Saccharomyces cerevisiae), a much more extensively studied organism, shows this isn’t a one-off case either. The yeast network is much larger (777 589 scored interactions across 6400 proteins in STRING v.9.1.), and the changes introduced by v.10.0. appear to be scaled accordingly — 237 427 yeast interactions were omitted in the update, and 399 836 new ones were added.

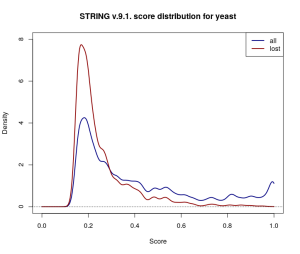
Kernel density estimates for the score distribution for yeast in STRING v.9.1. While the overall (navy) and discarded (dark red) score distributions differ from the ones for Borrelia Hermsii above, a similar trend of omitting more low-scored edges is observed.

So what causes over 30% of the scored interactions in the database to disappear into thin air? At least in part this may have to do with thresholding and small changes to the scoring procedure. STRING truncates reported interactions to those with a score above 0.15. Estimating how many low-scored interactions have been lost from the original dataset in this way is difficult, but the wide coverage of gene co-expression data would suggest that they’re a far from negligible proportion of the scored networks. The changes to the co-expression scoring pipeline in the latest release [1], coupled with the relative abundance of co-expression data, could have easily shifted scores close to 0.15 on the other side of the threshold, and therefore might explain some of the dramatic difference.

However, this still doesn’t account for changes introduced in other channels, or for interactions which have non-overlapping types of supporting evidence recorded in the two database versions. Moreover, thresholding at 0.15 adds a layer of uncertainty to the dataset — there is no way to distinguish between interactions where there is very weak evidence (i.e. score below 0.15), pairs of proteins that can be safely assumed not to interact (i.e. a “true” score of 0), and pairs of proteins for which there is simply no data available. While very weak evidence might not be of much use when studying a small part of the network, it may have consequences on a larger scale: even if only a very small fraction of these interactions are true, they might be indicative of robustness in the network, which can’t be otherwise detected.

In conclusion, STRING is a valuable resource of protein interaction data but one ought to take the reported scores with a grain of salt if one is to take a stochastic approach to protein interaction networks. Perhaps if scoring pipelines were documented in a way that made them reproducible and if the data wasn’t thresholded, we would be able to study the uncertainty in protein interaction networks with a bit more confidence.